What is a chord? (part two)

In part one, we learned about 3-note chords:

• the parts of a chord ( root, 3rd, 5th )
• different kinds of chords (major, minor, suspended, diminished, augmented)
• chords that belong to a scale or key (diatonic chords)

Here in part two, we are going to focus on how you can move these chords around to get so much more out of your playing. We’ll also look at ways to use these chords to improvise, and we’ll discover how melody is based on chords (a really important thing to understand!)

Inversions

What makes a C Chord a C Chord?

It has the notes C, E, G, and C is the root. Full stop, that’s it. Does it matter what order the notes are in? No! You can move the notes around. You can play them close together or far apart. You can split them between two hands. As long as you have those three notes, it’s a C chord.

Inverting the Chord

Inverting the chord just means to take what was on the bottom and move it up an octave. (When I say bottom, I mean the leftmost, or lowest note. Top is the highest note, or the one on the right.)

In case you don’t know, an octave is the next highest note of the same letter. So if I go from one C to the next C, I’ve moved up one octave.

(Octa- means 8. If you count the white notes between C and C, including both C’s, you have 8 white notes.)

An octave of C

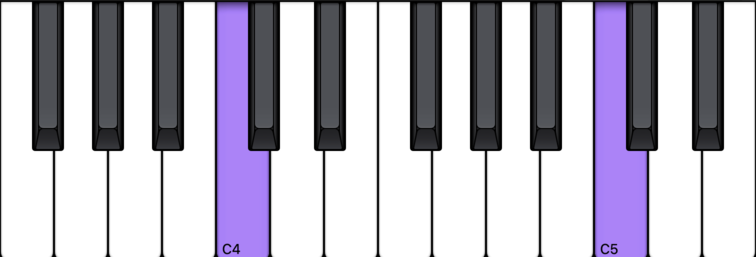
So far, we’ve been learning chords in root position. Root position means the root is the lowest note. Here’s C Major in root position:

1st Inversion

So, take the bottom note (in this case C), and move it up an octave to the higher C. You still have C, E, and G, but in a different order:

C Major Chord 1st Inversion

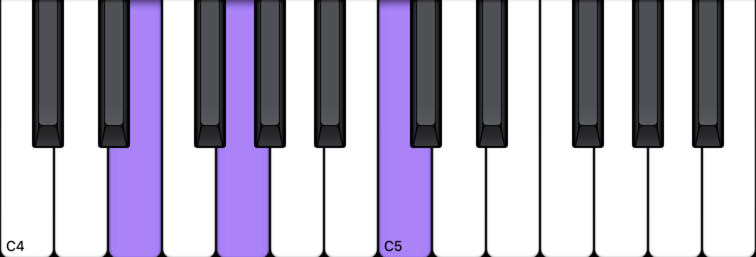
Et voilà! We have the first inversion of C major.

Note: A lot of my students will confuse the naming of this as “2nd position”. The first position is “root position”, where we started. But this inversion is the FIRST time we are INVERTING it, therefore it’s called first inversion.

Let’s see an example with D Major. Here it is in root position:

Think: why is this called root position again? (Answer further up the page.)

We take the leftmost (lowest, bottom) note, and move it up an octave:

D Major Chord 1st Inversion

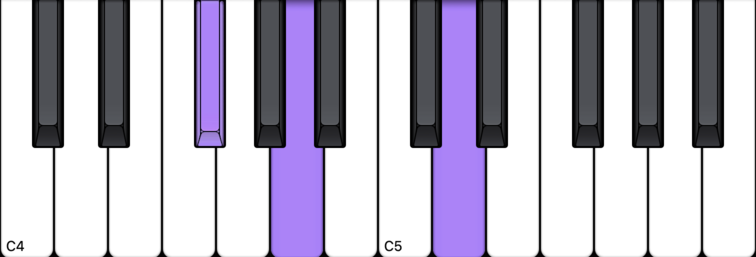
And there you have D Major in 1st inversion. Click here to see all major chords in 1st inversion.

Now, some of my students confuse the “root” of the chord for the bottom note in the chord. That’s only true in root position! In this case we have first inversion, where we have moved the D up an octave, and now the F# is on the bottom. But the D is still the root, the F# is still the 3rd, and the A is still the 5th.

2nd Inversion

Once we’re in 1st inversion, the next step is to learn 2nd inversion. To get to 2nd inversion, just repeat the process we did from root position to first inversion. Take C in first inversion:

C Major Chord 1st Inversion

What’s the bottom note? E. Move it up an octave:

C Major Chord 2nd Inversion

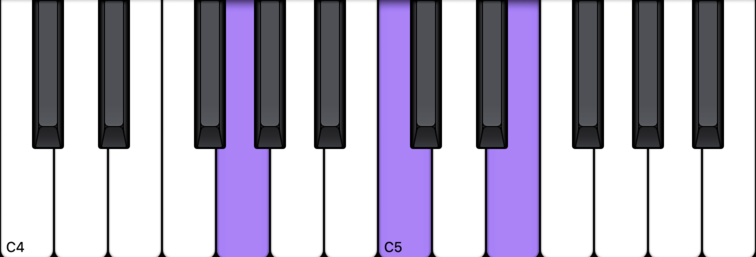
Easy peasy lemon squeezy! If you do this process one more time, what you end up with is the root position in C, but an octave higher than where you started. Here’s a video to show you what I mean:

How many positions are there for a chord?

However many notes there are in the chord, that’s how many positions there are. So for triads, which have three notes, we have three positions: Root position, first inversion, second inversion.

For a note with 4 chords, you’d have 4 positions: Root, first, second, third.

So long as the notes are all as close together as they can be for that chord, and you didn’t skip any chord tones, the number of positions is the same as the number of notes in the chord. And that brings me to my next point…

Close Position vs. Open Position

A “close” position of a chord happens when you haven’t skipped any chord tones in between what you’re playing. So, the chord C has the notes (“chord tones”) C E G:

A “chord tone” is just a note that belongs to a chord.

In this case, I didn’t skip any C’s, E’s, or G’s to get from the the C to the E or the E to the G. Let me show you what happens when we take the E up an octave:

C Major Open Position

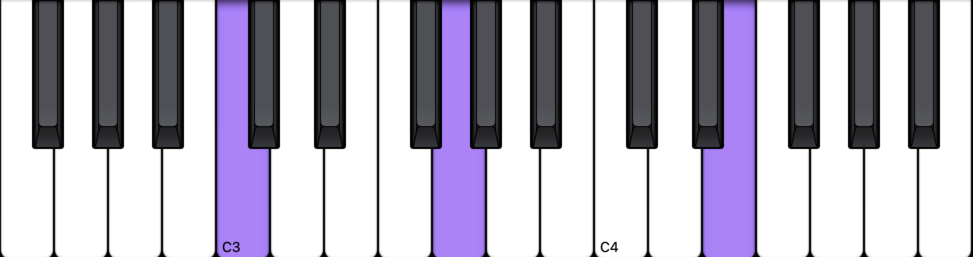
Ah, now from the highlighted C to the highlighted G, we’ve skipped E – which was one of the chord tones. We’re now in an open position instead of a close position. You’ll notice we also skip another C (labeled C4 in the picture) between the G and the E.

When we’re studying root positions and inversions, those are all close position. We know there are only 3 positions for a 3 note chord, because once you’ve gone from Root to 1st to 2nd inversion, if you go up again you’re back to Root position.

A Better Way to Change Chords Using Inversions

Listen to the sound of these two examples, where I play the same chords in the same order.

Chords: C, F, C, G, C

In this version, I’m going to play only root positions:

And in this version, I’ll play the same chords using inversions for F and G:

Sometimes, you’ll want the first way. But most of the time, you’ll want to play using inversions. I hope you’ll agree with me that the second way created a smoother sound, since the notes didn’t jump up but instead just moved right next door.

When you play with inversions, you’ll also notice that your hand doesn’t have to move as much, since the notes are all right next to each other.

To figure out the shortest way to get to the next chord, you have to figure out the common tones. Common tone is a fancy phrase that means “a note that two chords have in common”.

Take the chord C, for instance:

The notes are C, E, and G. Now let’s say F major is where you want to go next. What are the notes in F?

F, A, C. So, which of these letters shows up in both the C chord and the F chord?

The answer is C. Since that’s the common tone, leave it alone and move the other two notes up. If you played a C Major chord you probably had a thumb on the C note. So, leave the thumb there and move the other two notes up (E and G move up to F and A).

F Major Chord 2nd Inversion

Let’s repeat the process for the C chord to the G chord.

C major has C E G.

G major has G B D.

The common tone is G. So, leave the common tone alone. Move the other notes.

G Major Chord 1st Inversion

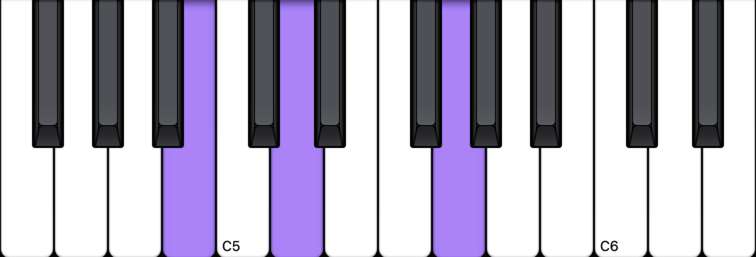
As you can see, the B-D of the G chord were right next door to the C-E of the C chord. Scroll back up and watch the 2nd video again and see if it makes more sense to you now.

Chords With Two Common Tones

If you’re looking at two 3-note chords, they can share 0 common tones, or 1, or 2. So far, we’ve seen chords that shared one common tone.

Let’s look at chords that share two common tones. For instance, C and A minor:

C to Am by root movement

C has the notes “C E G”

Am has the notes “A C E”

C and E are both common tones. That leaves the last note – G from the C chord, or A from the Am chord. So, we can leave the common tones alone and move G to A like so:

C to Am by inversion