Half Steps and Whole Steps on the Piano

In this article we’re going to look at how to hit each note on the piano in order, without skipping any. We’ll define half steps and whole steps, which are really important to understanding how to build chords and scales, which are the foundational blocks of music!

Playing All the Notes In Order

Here are all 12 notes played in order on piano. Most of the time you go from white to black or black to white, but notice from note E to F – there’s no black note in between. In that case, it’s white to white. (Same goes for B to C, which isn’t shown in this video.)

The word chromatic describes this process – moving from one note to the very next note. You’ll hear things like “that’s a chromatic scale” or “that part moves chromatically”.

Half Steps

If you move from one note to the very next note on the piano, you’re moving by a half step. In other words, a half step is the distance from one note to the very next note (whether white or black).

In two cases, a white note to a white note is a half step: E to F, and B to C. Every other half step is black to white or white to black.

Here are three examples of half steps:

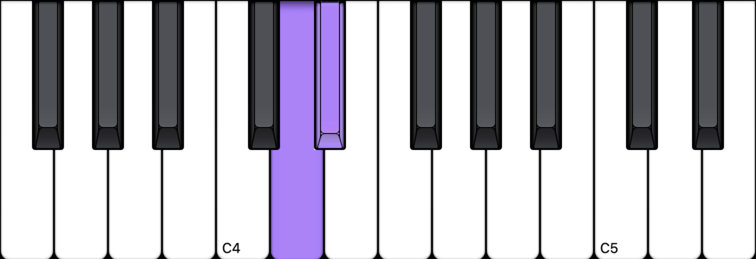
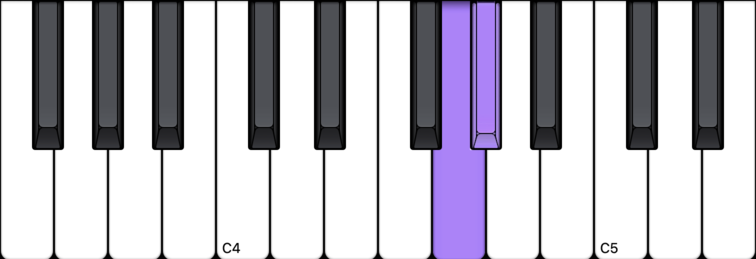
Whole Steps

Two halves make a whole, right? So if you move two half steps, that’s the same as saying you’ve moved a whole step.

A whole step is equal to two half steps.

Take any two black notes that have ONLY one white note in between – those two black notes are a whole step apart.

Two black notes with only one white note in between is a whole step (example 1)

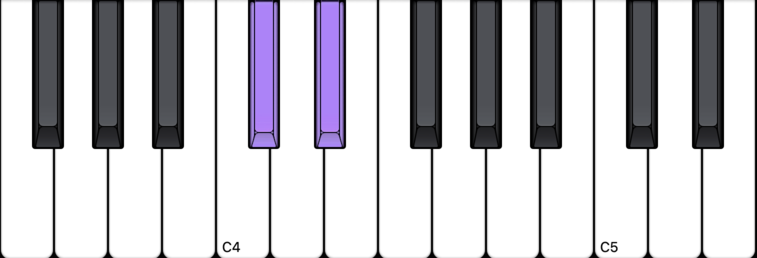
Two black notes with only one white note in between is a whole step (example 2)

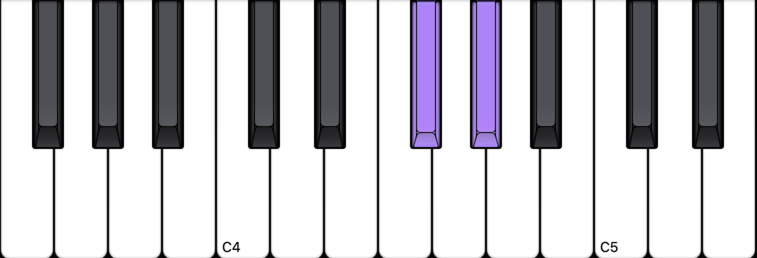
Take any two white notes that have ONLY one black note in between – those two white notes are a whole step apart.

A to B is a whole step

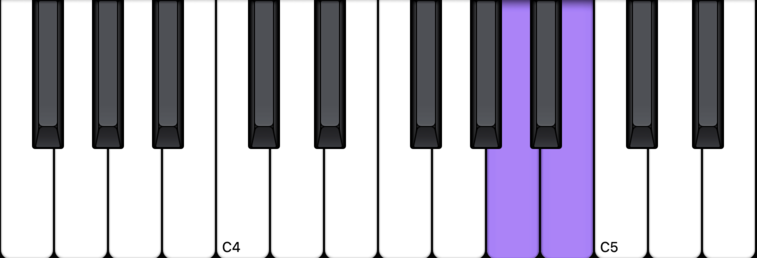
D to E is a whole step

Most of the time, a whole step is from white to white or black to black, but there are four cases where it’s white to black or black to white:

From E up a whole step

From F down a whole step

From B up a whole step

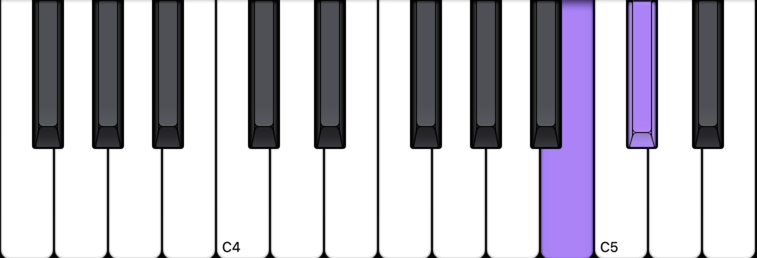
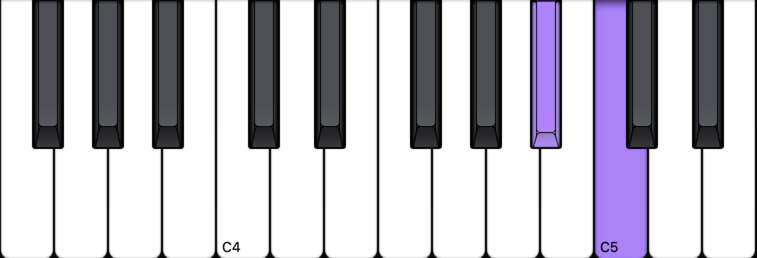
From C down a whole step

Sharps and Flats

Have you ever heard someone tell a singer they’re a little flat? Or sharp? Let’s talk about those words.

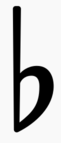
Sharp means to go up one half step.

Flat means to go down one half step.

Natural is used when we want to specify that we’re going back to the original note. So, a piece of music tells you to play F sharp (F#), but shortly after wants you to play the regular white key F, they’ll call it F natural (F♮).

Naturals are always white keys on piano.

So, next time you hear someone say “you’re a little flat”, you’ll know what they mean! They haven’t quite come up to the pitch of the note.

Naming the Black Notes

“Sharp” and “Flat” are not just directions to move up or down; they’re also the way we name the black notes.

Take F. Go up a half step (sharp it). You’re now on the first black note in a set of three. This note is called F sharp (F#).

F# note (F sharp)

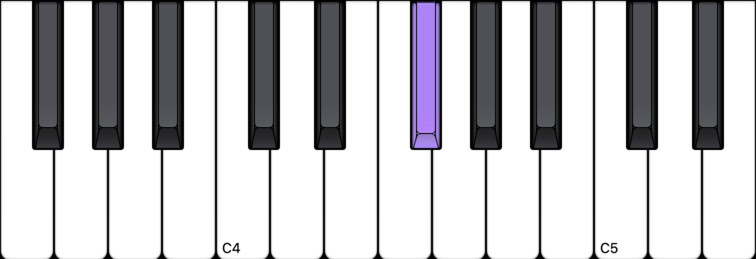
So it follows that these other notes are G#, A#, C#, D#:

G# note (G sharp)

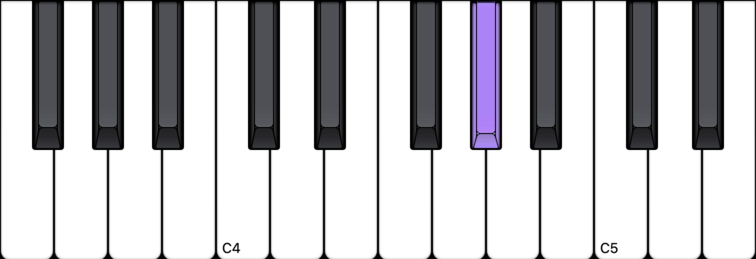
A# note (A sharp)

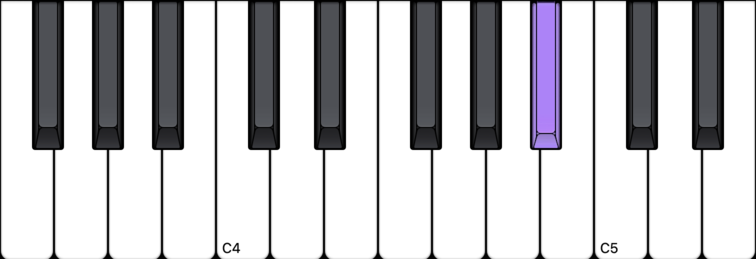
C# note (C sharp)

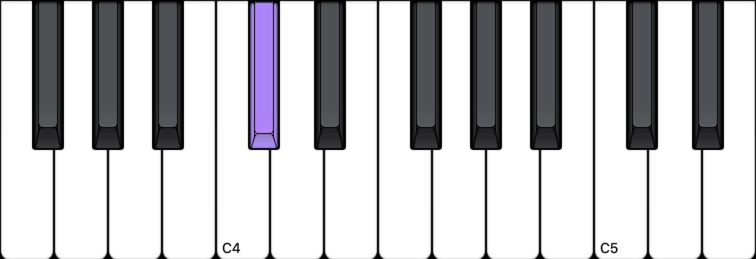
D# note (D sharp)

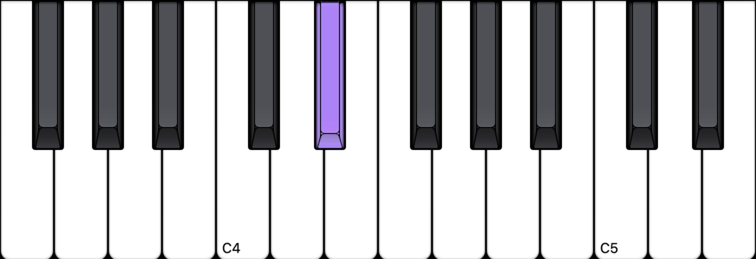
Here’s the kicker… all of these black notes can also be named by their flat names. For instance, that first note in the set of three black notes – we called that one F# earlier. But, if you think of G and go down one from there (flat it), you end up on the same note! So, F# could also be Gb.

Gb (G flat)

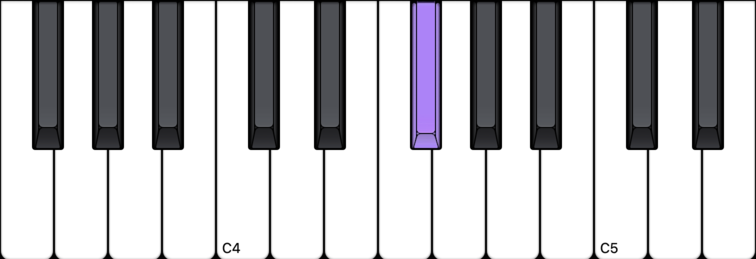
Table of Notes Showing Both Names (Enharmonics)

Here are the black notes listed with both of their names.

The concept that there are two names for the same note is called enharmonics. C# is the enharmonic name for Db.

Sharp name	Equivalent Flat name
C#	Db
D#	Eb
F#	Gb
G#	Ab
A#	Bb

You should be aware that there is such a thing as an E# (which we’d usually call F), a B# (C), an Fb (E), and a Cb (B). Since you’re just learning about sharps and flats now, you don’t need to spend much time thinking about these white notes with sharp and flat names – just be aware that they exist.